向量搜索算法基础

向量相似性搜索（Similarity Search）是向量数据库的核心功能，通过计算向量间的相似度或距离，快速从海量数据中找到目标数据点。例如：在电商平台中，向量相似性搜索是“猜你喜欢”等推荐功能的核心引擎。其工作流程通常如下：首先，利用深度学习模型分别生成用户向量和商品向量。用户向量基于其历史行为（如浏览、购买记录）生成，商品向量则从其属性（如标题、描述、图片）中提取。接着，将所有商品向量存入向量数据库，并为其构建高效的索引。当用户访问平台时，系统会将该用户的向量作为查询条件，在向量数据库中快速搜索与之最相似的若干商品向量，从而实现个性化推荐。这种基于向量语义相似度的推荐，比传统方法更能理解用户的潜在偏好。

那么问题来了，怎么定义这个向量相似性呢？我们抽像成一个数学问题，现在给定一个查询向量 q，在一个庞大的向量集合 {v_1, v_2, ..., v_n}（通常 n 在百万到十亿甚至万亿级）中，快速找到与 q 最相似的前 K 个向量（K-nearest neighbors, KNN）。

1.向量相似性度量

1.1欧氏距离

聪明的你想到，我可以直接计算2个向量之间的距离，如果向量之间的距离越小，则表示越相似。恭喜你，你发明了欧氏距离算法。

公式

dist (q, v) = ∥ q - v ∥_{2} = \sqrt{\sum_{i = 1}^{n} (q_{i} - v_{i})^{2}}

特点

计算两点之间的直线距离
适用于需要物理距离真实感的场景（如图像特征匹配）
计算前通常需要对向量进行L2归一化处理
距离值越小表示越相似，取值范围为 [0, +∞)

1.2内积 (点积)

聪明的你继续发现，除了直接计算距离，还可以从“方向”的角度衡量向量的相似性：如果两个向量的方向越接近，它们的夹角越小，则它们越相似。恭喜你，你抓住了点积的核心思想，发明了内积算法。点积通过计算两个向量在方向上的对齐程度来衡量相似性。

公式

sim (q, v) = q^{⊤} v = \sum_{i = 1}^{n} q_{i} v_{i}

特点

数值越大表示越相似
常见于深度学习模型输出的Embedding向量相似度计算
使用时通常需要对向量进行归一化处理
取值范围为 (-∞, +∞)，但归一化后通常在有限范围内

1.3余弦相似度

聪明的你又发现，仅仅用内积衡量还不够，因为向量的长度会影响结果。那如果我们只关注方向，而忽略长度呢？恭喜你，你又发明了余弦相似度算法。它通过计算两个向量夹角的余弦值来度量相似性，值越接近 1，说明方向越一致，越相似。

公式

\cos (q, v) = \frac{q^{⊤} v}{∥ q ∥_{2} ∥ v ∥_{2}} = \frac{\sum_{i = 1}^{n} q_{i} v_{i}}{\sqrt{\sum_{i = 1}^{n} q_{i}^{2}} \sqrt{\sum_{i = 1}^{n} v_{i}^{2}}}

特点

衡量向量方向的相似性，忽略向量的长度（模）
本质上是内积在L2归一化后的特例：当 $∥ q ∥ = ∥ v ∥ = 1$ 时， $\cos (q, v) = q^{T} \cdot v$
广泛用于文本、语义相似度计算等领域
在向量索引构建前进行归一化是标准操作流程
取值范围为 [-1, 1]，值越大表示越相似

2.向量搜索算法

2.1暴力搜索算法

现在我们知道了怎么评估向量之间的相似度，那么会到问题本身，怎么从一个庞大的向量集合 {v_1, v_2, ..., v_n}（通常 n 在百万到十亿甚至万亿级）中，快速找到与 q 最相似的前 K 个向量，聪明的你想到可以遍历这n个向量，并计算每个向量与查询向量的相似度或距离，最后返回最相似的前K个向量。恭喜你，发明了暴力搜索算法。暴力搜索是最简单、最直接的向量相似性检索方法，其基本原理是计算查询向量与数据库中所有向量的相似度或距离，返回最接近的k个结果。这种方法不依赖任何预先构建的索引，因此能够保证检索结果的精确性。

我们来简单的看看暴力搜索算法吧，假定我们要使用欧式距离，使用scipy工具包进行计算。

python

import numpy as np
from scipy.spatial.distance import cdist
import time

def generate_sample_data(num_vectors=1000, vector_dim=64, num_queries=5):
    """
    生成示例向量数据
    :param num_vectors: 数据库向量数量
    :param vector_dim: 向量维度
    :param num_queries: 查询向量数量
    :return: 数据库向量和查询向量
    """
    print("=== 步骤1: 数据生成 ===")
    print(f"生成 {num_vectors} 个 {vector_dim} 维数据库向量和 {num_queries} 个查询向量...")
    
    # 设置随机种子保证结果可重现
    np.random.seed(42)
    
    # 生成数据库向量（模拟已有数据）
    database_vectors = np.random.randn(num_vectors, vector_dim).astype(np.float32)
    
    # 生成查询向量（模拟需要搜索的目标）
    query_vectors = np.random.randn(num_queries, vector_dim).astype(np.float32)
    
    print(f"数据库向量形状: {database_vectors.shape}")
    print(f"查询向量形状: {query_vectors.shape}")
    
    # 显示前3个向量的前5个维度作为示例
    print("\n数据库向量示例（前3个向量的前5维）:")
    for i in range(3):
        print(f"向量{i}: {database_vectors[i, :5]}")
    
    print("数据生成完成!\n")
    
    return database_vectors, query_vectors

def euclidean_distance_manual(vec1, vec2):
    """
    手动计算两个向量之间的欧氏距离（教学演示）
    欧氏距离公式: d = √(Σ(x_i - y_i)²) [3,5](@ref)
    """
    # 确保向量维度相同
    assert len(vec1) == len(vec2), "向量维度必须相同"
    
    # 计算差的平方和
    squared_diff = np.sum((vec1 - vec2) ** 2)
    
    # 开平方根得到欧氏距离
    distance = np.sqrt(squared_diff)
    
    return distance

def brute_force_search_cdist(database_vectors, query_vectors, k=3):
    """
    使用cdist实现暴力搜索[6,7](@ref)
    :param database_vectors: 数据库向量矩阵 (n_samples, n_features)
    :param query_vectors: 查询向量矩阵 (n_queries, n_features)  
    :param k: 返回最近邻的数量
    :return: 距离矩阵和索引矩阵
    """
    print("=== 步骤2: 距离计算（使用cdist） ===")
    print(f"计算 {len(query_vectors)} 个查询向量与 {len(database_vectors)} 个数据库向量的欧氏距离...")
    
    start_time = time.time()
    
    # 使用cdist计算所有查询向量与所有数据库向量的欧氏距离[6](@ref)
    # 返回形状为 (n_queries, n_database) 的距离矩阵
    distance_matrix = cdist(query_vectors, database_vectors, metric='euclidean')
    
    calculation_time = time.time() - start_time
    print(f"距离矩阵计算完成! 耗时: {calculation_time:.4f} 秒")
    print(f"距离矩阵形状: {distance_matrix.shape} (查询数量 × 数据库数量)")
    
    # 对每个查询向量，找到距离最小的k个向量的索引[1](@ref)
    print("\n=== 步骤3: 结果排序 ===")
    sort_start_time = time.time()
    
    # argsort默认按升序排序，前k个就是最小的k个距离
    nearest_indices = np.argsort(distance_matrix, axis=1)[:, :k]
    
    # 提取对应的距离值
    nearest_distances = np.take_along_axis(distance_matrix, nearest_indices, axis=1)
    
    sort_time = time.time() - sort_start_time
    print(f"排序完成! 耗时: {sort_time:.4f} 秒")
    print(f"返回每个查询向量的前 {k} 个最近邻")
    
    total_time = calculation_time + sort_time
    print(f"总耗时: {total_time:.4f} 秒\n")
    
    return distance_matrix, nearest_indices, nearest_distances

def demonstrate_single_calculation(database_vectors, query_vectors):
    """
    演示单个向量的距离计算过程（教学目的）
    """
    print("=== 手动计算演示 ===")
    
    # 使用第一个查询向量和第一个数据库向量进行演示
    query_vec = query_vectors[0]
    db_vec = database_vectors[0]
    
    print("查询向量（前10维）:", query_vec[:10])
    print("数据库向量（前10维）:", db_vec[:10])
    
    # 手动计算距离
    manual_distance = euclidean_distance_manual(query_vec, db_vec)
    
    # 使用cdist计算距离
    cdist_distance = cdist([query_vec], [db_vec], metric='euclidean')[0][0]
    
    print(f"手动计算距离: {manual_distance:.6f}")
    print(f"cdist计算距离: {cdist_distance:.6f}")
    
    # 验证结果是否一致
    if np.isclose(manual_distance, cdist_distance):
        print("✓ 两种方法计算结果一致!")
    else:
        print("⚠ 计算结果存在差异")
    
    print()

def display_search_results(query_vectors, database_vectors, nearest_indices, nearest_distances, k=3):
    """
    显示搜索结果
    """
    print("=== 步骤4: 搜索结果展示 ===")
    
    for i in range(len(query_vectors)):
        print(f"\n查询向量 {i} 的最近邻 (前{k}个):")
        print("-" * 50)
        
        for j in range(k):
            idx = nearest_indices[i][j]
            dist = nearest_distances[i][j]
            
            # 显示向量的一些特征用于验证
            query_preview = query_vectors[i][:3]  # 前3维
            neighbor_preview = database_vectors[idx][:3]  # 前3维
            
            print(f"  最近邻 {j+1}:")
            print(f"    索引: {idx}")
            print(f"    距离: {dist:.6f}")
            print(f"    查询向量预览: {query_preview}...")
            print(f"    最近邻预览: {neighbor_preview}...")
        
        # 验证：手动计算第一个最近邻的距离进行验证
        first_idx = nearest_indices[i][0]
        verification_dist = euclidean_distance_manual(query_vectors[i], database_vectors[first_idx])
        print(f"  验证距离: {verification_dist:.6f} (应与上面一致)")

def performance_analysis(database_vectors, query_vectors):
    """
    性能分析：比较不同数据规模下的计算时间
    """
    print("\n=== 性能分析 ===")
    
    # 测试不同数据规模
    sizes = [100, 500, 1000]
    
    for size in sizes:
        if size > len(database_vectors):
            continue
            
        subset_db = database_vectors[:size]
        subset_query = query_vectors[:min(3, len(query_vectors))]
        
        start_time = time.time()
        distance_matrix = cdist(subset_query, subset_db, metric='euclidean')
        nearest_indices = np.argsort(distance_matrix, axis=1)[:, :3]
        end_time = time.time()
        
        print(f"数据规模: {len(subset_db)} 个向量, 计算时间: {end_time - start_time:.4f} 秒")

def main():
    """
    主函数：演示暴力搜索的完整流程
    """
    print("向量暴力搜索实现 - 使用欧氏距离和cdist函数")
    print("=" * 60)
    
    # 1. 数据生成
    database_vectors, query_vectors = generate_sample_data(
        num_vectors=500000,    # 数据库向量数量
        vector_dim=1024,      # 向量维度
        num_queries=3       # 查询向量数量
    )
    
    # 2. 手动计算演示
    demonstrate_single_calculation(database_vectors, query_vectors)
    
    # 3. 使用cdist进行暴力搜索
    distance_matrix, nearest_indices, nearest_distances = brute_force_search_cdist(
        database_vectors, query_vectors, k=3
    )
    
    # 4. 显示搜索结果
    display_search_results(query_vectors, database_vectors, nearest_indices, nearest_distances)
    
    # 5. 性能分析
    performance_analysis(database_vectors, query_vectors)
    
    print("\n" + "=" * 60)
    print("暴力搜索总结:")
    print("✓ 精度: 100%准确（穷举所有可能性）")
    print("✓ 简单: cdist一行代码完成所有距离计算")
    print("⚠ 缺点: 计算复杂度O(N×M)，不适合大规模数据")
    print("💡 应用场景: 小规模数据集或精度要求极高的场景")

if __name__ == "__main__":
    main()

向量暴力搜索实现 - 使用欧氏距离和cdist函数
============================================================
=== 步骤1: 数据生成 ===
生成 500000 个 1024 维数据库向量和 3 个查询向量...
数据库向量形状: (500000, 1024)
查询向量形状: (3, 1024)

数据库向量示例（前3个向量的前5维）:
向量0: [ 0.49671414 -0.1382643   0.64768857  1.5230298  -0.23415338]
向量1: [1.7275431  0.43632367 0.03800348 0.12003133 0.613518  ]
向量2: [-0.32789472  0.15519068  0.8250983  -0.8671302  -0.65811646]
数据生成完成!

=== 手动计算演示 ===
查询向量（前10维）: [-0.3682938  -0.3867541  -1.5640609   0.14660783 -1.0207618   0.418243
  1.3014778  -0.6550172   0.9128868  -0.74166346]
数据库向量（前10维）: [ 0.49671414 -0.1382643   0.64768857  1.5230298  -0.23415338 -0.23413695
  1.5792128   0.7674347  -0.46947438  0.54256004]
手动计算距离: 43.849701
cdist计算距离: 43.849702
✓ 两种方法计算结果一致!

=== 步骤2: 距离计算（使用cdist） ===
计算 3 个查询向量与 500000 个数据库向量的欧氏距离...
距离矩阵计算完成! 耗时: 3.1119 秒
距离矩阵形状: (3, 500000) (查询数量 × 数据库数量)

=== 步骤3: 结果排序 ===
排序完成! 耗时: 0.0734 秒
返回每个查询向量的前 3 个最近邻
总耗时: 3.1852 秒

=== 步骤4: 搜索结果展示 ===

查询向量 0 的最近邻 (前3个):
--------------------------------------------------
  最近邻 1:
    索引: 142794
    距离: 41.003796
    查询向量预览: [-0.3682938 -0.3867541 -1.5640609]...
    最近邻预览: [-1.0047811   1.1266526  -0.02369397]...
  最近邻 2:
    索引: 405941
    距离: 41.031636
    查询向量预览: [-0.3682938 -0.3867541 -1.5640609]...
    最近邻预览: [ 0.42480972 -0.22937793  0.12584493]...
  最近邻 3:
    索引: 273766
    距离: 41.065637
    查询向量预览: [-0.3682938 -0.3867541 -1.5640609]...
    最近邻预览: [0.36528045 0.1361699  0.1045911 ]...
  验证距离: 41.003796 (应与上面一致)

查询向量 1 的最近邻 (前3个):
--------------------------------------------------
  最近邻 1:
    索引: 316188
    距离: 41.585471
    查询向量预览: [-0.25062057  0.04495366  0.4566647 ]...
    最近邻预览: [ 2.391179   -1.36612     0.72082907]...
  最近邻 2:
    索引: 353285
    距离: 41.606924
    查询向量预览: [-0.25062057  0.04495366  0.4566647 ]...
    最近邻预览: [-0.33884752 -0.11371469 -0.30244926]...
  最近邻 3:
    索引: 271899
    距离: 41.669258
    查询向量预览: [-0.25062057  0.04495366  0.4566647 ]...
    最近邻预览: [-0.6639867  -0.07316009  0.7632062 ]...
  验证距离: 41.585468 (应与上面一致)

查询向量 2 的最近邻 (前3个):
--------------------------------------------------
  最近邻 1:
    索引: 385729
    距离: 40.337883
    查询向量预览: [ 0.1009455   0.4344626  -0.65966547]...
    最近邻预览: [-0.77918327 -0.04902988 -0.3034025 ]...
  最近邻 2:
    索引: 304670
    距离: 40.442426
    查询向量预览: [ 0.1009455   0.4344626  -0.65966547]...
    最近邻预览: [-0.70693696 -0.31210005  0.29609913]...
  最近邻 3:
    索引: 153981
    距离: 40.539462
    查询向量预览: [ 0.1009455   0.4344626  -0.65966547]...
    最近邻预览: [ 0.08247662  1.0076854  -0.2868992 ]...
  验证距离: 40.337883 (应与上面一致)

=== 性能分析 ===
数据规模: 100 个向量, 计算时间: 0.0009 秒
数据规模: 500 个向量, 计算时间: 0.0044 秒
数据规模: 1000 个向量, 计算时间: 0.0064 秒

============================================================
暴力搜索总结:
✓ 精度: 100%准确（穷举所有可能性）
✓ 简单: cdist一行代码完成所有距离计算
⚠ 缺点: 计算复杂度O(N×M)，不适合大规模数据
💡 应用场景: 小规模数据集或精度要求极高的场景

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314

代码使用了高效的scipy函数计算距离，并通过排序快速提取最近邻结果，适用于小规模数据或精确匹配场景。

2.2维度搜索灾难

暴力搜索虽然简单，但计算代价较高，尤其在数据规模增大时，计算所有距离的复杂度会迅速增加。同时，维度较高的时候，会出现“维度灾难”的情况。由高维空间几何与统计性质带来的不友好现象，直接破坏距离、密度、采样的直觉，从而让很多算法（包括最近邻搜索）失效或效率极差。

在低维时（二维 / 三维），点之间的距离差异明显，近的就近，远的就远；而在高维时，大多数点彼此都“差不多远”，空间迅速变得稀疏。导致传统算法在高维场景中的性能退化，这种现象被称为“维度灾难”

那么我来直观的看一下高维数据的情况下，点之间的距离差异是如何变化的。

python

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 中文字体
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

def simulate_distances(dimensions, n_points=500, seed=42):
    """模拟不同维度下的点间距离分布"""
    np.random.seed(seed)
    results = {}
    for d in dimensions:
        data = np.random.rand(n_points, d)
        q = np.random.rand(1, d)
        distances = np.linalg.norm(data - q, axis=1)
        results[d] = distances
    return results

def plot_all(results):
    """综合绘制：分布直方图 + min/max/mean + 最近邻比值"""
    dims = sorted(results.keys())
    min_d, max_d, mean_d, ratio = [], [], [], []

    for d in dims:
        dist = results[d]
        min_d.append(dist.min())
        max_d.append(dist.max())
        mean_d.append(dist.mean())
        ratio.append(dist.min() / dist.mean())

    fig, axes = plt.subplots(2, 2, figsize=(14, 10))
    colors = ["#1f77b4", "#ff7f0e", "#2ca02c", "#9467bd", "#d62728", "#17becf"]

    # 子图1：不同维度的距离分布
    for i, (d, dist) in enumerate(results.items()):
        axes[0, 0].hist(dist, bins=30, alpha=0.6, color=colors[i % len(colors)], label=f"{d}维")
    axes[0, 0].set_title("不同维度下点到查询点的距离分布", fontsize=14)
    axes[0, 0].set_xlabel("欧氏距离", fontsize=12)
    axes[0, 0].set_ylabel("频数", fontsize=12)
    axes[0, 0].legend()
    axes[0, 0].grid(True, linestyle="--", alpha=0.6)

    # 子图2：最小/最大/平均距离随维度变化
    axes[0, 1].plot(dims, min_d, "o-", color="#1f77b4", linewidth=2, markersize=6, label="最近距离")
    axes[0, 1].plot(dims, max_d, "s-", color="#ff7f0e", linewidth=2, markersize=6, label="最远距离")
    axes[0, 1].plot(dims, mean_d, "^-", color="#2ca02c", linewidth=2, markersize=6, label="平均距离")
    axes[0, 1].set_title("维度灾难：距离随维度变化趋势", fontsize=14)
    axes[0, 1].set_xlabel("维度", fontsize=12)
    axes[0, 1].set_ylabel("距离", fontsize=12)
    axes[0, 1].legend()
    axes[0, 1].grid(True, linestyle="--", alpha=0.6)

    # 子图3：最近邻/平均距离比值
    axes[1, 0].plot(dims, ratio, "d-", color="red", linewidth=2, markersize=6, label="比值")
    axes[1, 0].axhline(1, color="gray", linestyle="--", linewidth=1)  # 参考线 y=1
    axes[1, 0].set_title("维度灾难：最近邻与平均点几乎一样远", fontsize=14)
    axes[1, 0].set_xlabel("维度", fontsize=12)
    axes[1, 0].set_ylabel("最近邻 / 平均距离", fontsize=12)
    axes[1, 0].set_ylim(0, 1.05)
    axes[1, 0].grid(True, linestyle="--", alpha=0.6)
    axes[1, 0].legend()

    # 子图4：文字解释
    axes[1, 1].axis("off")
    explanation = (
        "直观结论：\n"
        "1. 随着维度升高，所有点到查询点的距离都在增大；\n"
        "2. 最近邻距离逐渐接近平均距离；\n"
        "3. 高维空间里点之间差别越来越小，距离失去区分能力。\n\n"
        " 这就是维度灾难的本质"
    )
    axes[1, 1].text(0.05, 0.5, explanation, fontsize=13, va="center")

    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    dimensions = [2, 10, 50, 100, 500, 1000]
    results = simulate_distances(dimensions, n_points=1000)
    plot_all(results)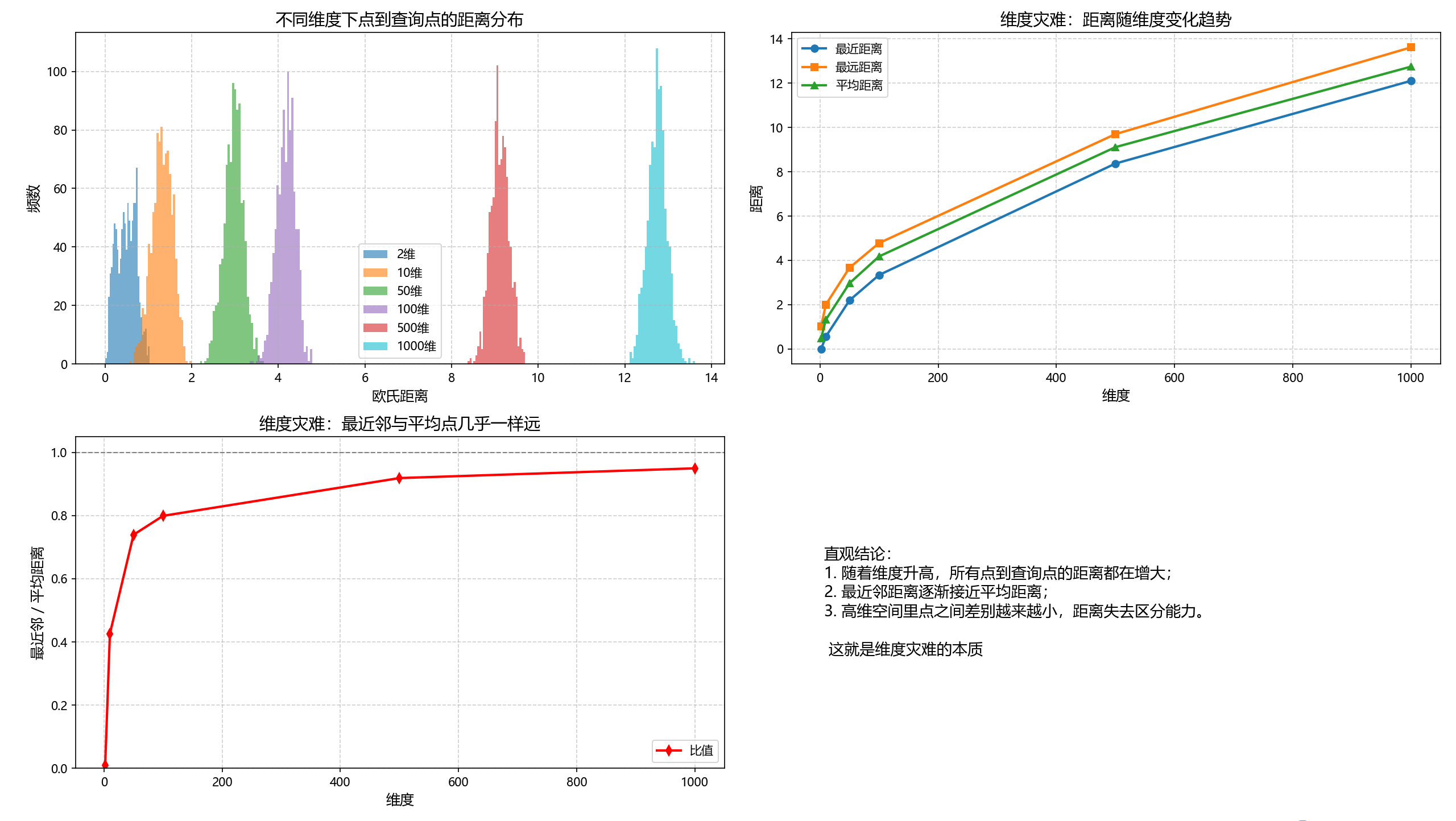

alt text

从左上角的图中可以看到，在低维空间（如 2 维），点到查询点的距离差异很大：有的点很近，有的点很远。随着维度升高，所有点的距离都集中在一个狭窄的区间内，看起来几乎一样远。高维空间里，距离的差异正在被“抹平”。
从右上角的图可以看到，最小 / 最大 / 平均距离随维度变化，随着维度增加，所有点的距离都在变大。更重要的是，最近邻距离逐渐接近平均距离，两者差别越来越小。在高维空间里，最近邻其实并不比普通点更近多少。
从左下角的图可以看到，最近邻 / 平均距离比值，在低维时，比值明显小于 1，说明最近邻和平均点差别大。在高维时，比值逐渐逼近 1，说明最近邻和普通点几乎一样远。这说明，高维空间中，单靠“距离”几乎无法区分点的远近。

聪明的你总结了这样的规律：

距离整体越来越大；
最近邻逐渐接近平均点；
距离失去区分能力；恭喜你，你发现了维度灾难（Curse of Dimensionality）的本质。

看到这里，聪明的你突然有顿悟了，前面用的方法都是欧式距离来评估相似度，那是因为方法不对，要是用其他的评估方法，比如点积或者余弦相似度就不会出现这种情况。

未完待续，继续更新中...

3.ANN搜索算法

聪明的你已经知道暴力搜索是如何工作的：遍历全部向量、计算相似度、选出最相似的 K 个。这当然是正确的，但当 n = 百万 / 亿 / 万亿时——恭喜你，你会发现电脑会给你一个长长的白眼(你这是准备累死我嘛)。聪明的你又想到，我能否对数据进行提前分类，这样

什么是ANN搜索？ ANN（Approximate Nearest Neighbors）搜索是一种用于在高维空间中快速查找最近邻的算法。与暴力搜索不同，ANN搜索通过引入近似计算，在保持较高召回率的同时，显著减少了计算复杂度。ANN的核心价值在于解决了"维度灾难"问题——当数据维度和数量增加时，暴力搜索的计算复杂度呈指数级增长，而ANN通过巧妙的近似方法维持了可接受的搜索性能。

未完待续，继续更新中...

向量搜索算法基础 ​

1.向量相似性度量 ​

1.1欧氏距离 ​

1.2内积 (点积) ​

1.3余弦相似度 ​

2.向量搜索算法 ​

2.1暴力搜索算法 ​

2.2维度搜索灾难 ​

3.ANN搜索算法 ​