向量数据的存储优化与GPU加速检索

近似最近邻搜索（ANNS）已成为数据库和人工智能基础设施的关键组成部分。不断增长的向量数据集给 ANNS 服务在性能、成本和准确性方面带来了重大挑战。现有 ANNS 系统均无法同时解决这些问题。

高维空间中的近似最近邻搜索(ANNS)旨在找出与给定查询向量最相似的前 k 个向量。该技术在数据挖掘、搜索引擎以及 AI 驱动的推荐系统等诸多领域具有广泛应用。特别是在大型语言模型(LLMs)近期蓬勃发展的推动下，ANNS 系统已成为现代 AI 基础设施的关键组成部分。

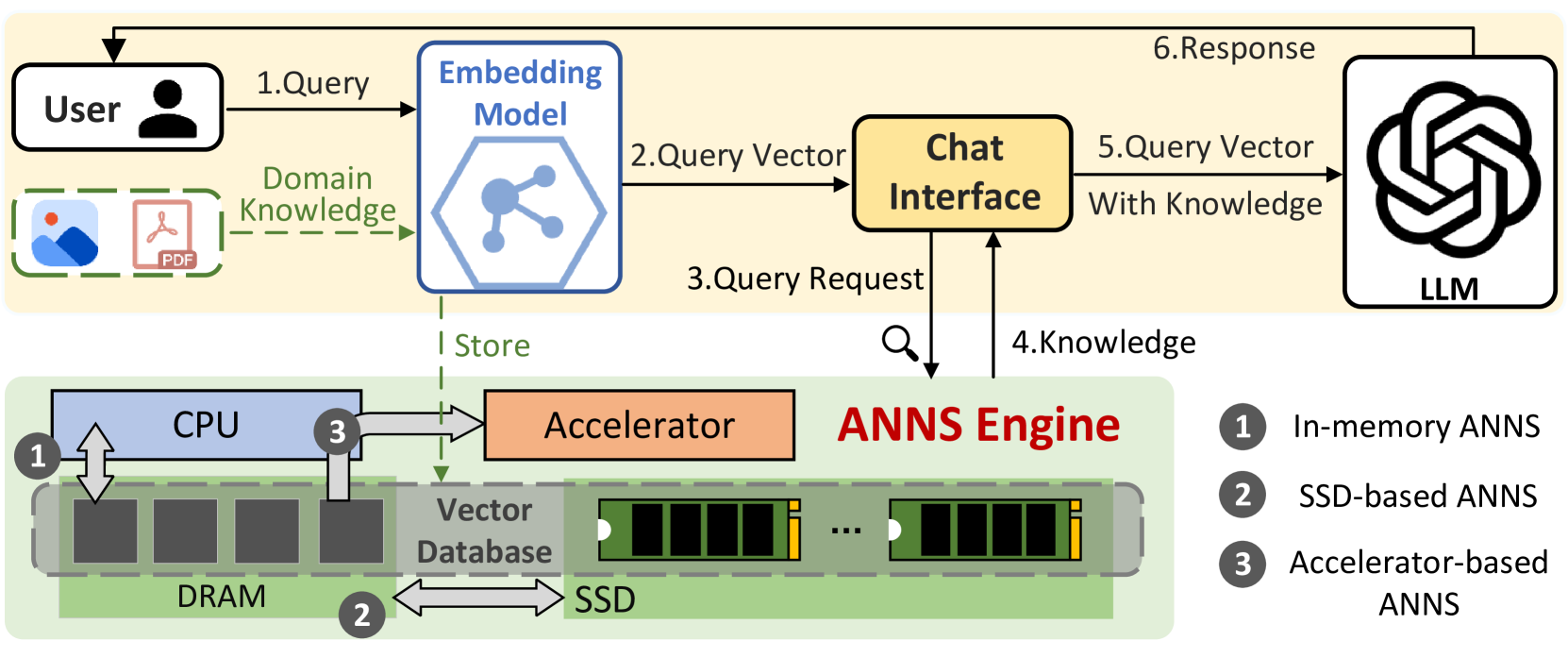
alt text

检索增强生成(RAG)的典型框架：领域特定知识首先被嵌入为高维向量并存储于向量数据库中。当聊天机器人接收到查询时，会通过 ANNS 引擎从向量数据库中检索最相关的知识，使 LLM 能够将这些知识作为额外上下文进行更精准的推理。

近似最近邻搜索（Approximate Nearest Neighbor Search, ANNS）是处理海量图片、文本特征等数据的核心技术。它的目标并非追求绝对最匹配的结果，而是通过高效方法获取足够相似的候选集。在实际应用中，这项技术面临着内存消耗巨大与计算强度极高两大严峻挑战。

1. 内存消耗

为了加速搜索过程，ANNS 系统需要预先构建类似 “目录” 或 “关系网” 的索引结构。详细内容请回到Milvus 索引介绍中IVF系列和HNSW系列。

然而，当数据量攀升至十亿甚至千亿级别的规模时，这些索引自身就会占用 TB 级别（相当于数个大型硬盘）的内存空间。如此高昂的内存成本，极大地限制了 ANNS 技术向更大规模数据处理场景的扩展。

2. 计算强度

ANNS 的核心操作是进行距离计算，即计算数据点之间的相似度，例如比较两张图片特征向量的差异。在处理高维数据（每个数据点包含数百甚至数千个特征值）和超大基数数据时，系统需要执行海量的距离计算，这对算力形成了巨大压力，使得计算强度极高。

在当下热门的检索增强生成（RAG）场景中，ANNS 扮演着至关重要的角色，它是支撑大语言模型（Large Language Model, LLM）实时检索外部知识的核心环节。实际测试数据显示，在整个 LLM 查询流程中，ANNS 阶段所消耗的时间接近 50%，已然成为制约系统响应速度的关键瓶颈。

3. 优化方法

为降低近似最近邻搜索(ANNS)的内存开销，现有方法主要分为两类：层次化索引(Hierarchical Indexing, HI)与乘积量化(Product Quantization, PQ)。

首先，层次化索引通过将索引存储于固态硬盘(SSD)来减少内存占用。以微软商用 ANNS 系统 SPANN为例，该系统将所有基于倒排文件(IVF)的索引（即倒排列表）存放于 SSD，仅通过导航图在内存中维护这些倒排列表的质心。虽然 SPANN 实现了低延迟，但我们发现其并发查询吞吐量存在明显瓶颈，在高端 SSD 上仅能支持最多四个 CPU 线程的峰值性能。这种有限的可扩展性制约了其在需要高吞吐量 AI 应用中的实用性。
其次，乘积量化是另一种有效降低内存成本的技术。该向量压缩方法可将高维向量的内存占用量减少高达 95%，同时还能将 ANNS 速度提升数倍。但由于 PQ 属于有损压缩方案，更高的压缩率往往会导致查询精度下降。对于某些要求高准确率的场景，这种情况通常是不可接受的。

FusionANNS 系统介绍

FusionANNS 是一种创新的 CPU/GPU 协同处理架构，专为十亿级高维向量的近似最近邻搜索而设计。它旨在解决现有十亿级近似最近邻搜索系统普遍存在的性能瓶颈、高昂成本、精度与效率权衡以及协同设计缺失等问题。

1. 系统架构

FusionANNS 的核心思想是通过精妙的 CPU/GPU 协同过滤和重排序机制，最小化 CPU、GPU 和 SSD 之间的数据传输量（尤其是大块向量内容），从而突破 I/O 性能瓶颈。该架构包含以下三大创新设计：

多级索引：
- 数据分层存储：智能地将数据分布在不同存储层级，CPU 主机内存仅存储轻量级导航图和向量 ID 元数据；GPU 显存存储经乘积量化高度压缩的向量数据；SSD 存储原始向量数据，仅用于重排序。
- 协同过滤：查询时，CPU 遍历导航图找到 top-m 个最近邻的倒排列表，仅将向量 ID 发送给 GPU，GPU 直接从显存读取对应压缩向量进行距离计算，避免了 CPU 和 GPU 间传输庞大向量内容。
启发式重排序：
- 动态批处理与提前终止：将重排序过程拆分为多个小批次顺序执行。
- 轻量级反馈控制：每完成一个小批次，计算当前结果集与前一批次结果集的变化率，若连续 β 个批次的变化率低于阈值 ε，则提前终止重排序。
冗余感知 I/O 去重：
- 优化的 SSD 存储布局：将与同一聚类中心最接近的多个原始向量紧凑打包存储在同一 SSD 页面。
- 两级去重：批次内合并访问同一 SSD 页面的多个向量请求；批次间利用内存缓冲区缓存已读取页面，避免重复 SSD I/O。

2. 性能优势

FusionANNS 通过上述协同设计，相比现有最先进的方案（基于 SSD 的 SPANN 和 GPU 加速的全内存 RUMMY）展现出显著优势：

超高吞吐量：相比 SPANN 提升 9.4 - 13.1 倍，相比 RUMMY 提升 2.4 - 4.9 倍。
低成本高效率：相比 SPANN 提升 5.7 - 8.8 倍，相比 RUMMY 提升 2.3 - 6.8 倍。
低延迟：实现超高吞吐量的同时，保持与 SPANN 相当的低查询延迟，远低于 RUMMY 在高并发或大向量数据集上的延迟。
卓越的可扩展性：随着 CPU 线程数增加，吞吐量能持续线性增长至 64 线程甚至更高。
显著降低内存需求：主机内存需求大幅降低，内存效率提升显著，如在 DEEP1B 数据集上比 RUMMY 高 32.4 倍。
高性价比硬件：仅需一个入门级 GPU（如 NVIDIA V100 32GB）和配备 SSD 的通用服务器即可支持十亿级数据集，硬件成本远低于全内存 GPU 方案。

流程详解

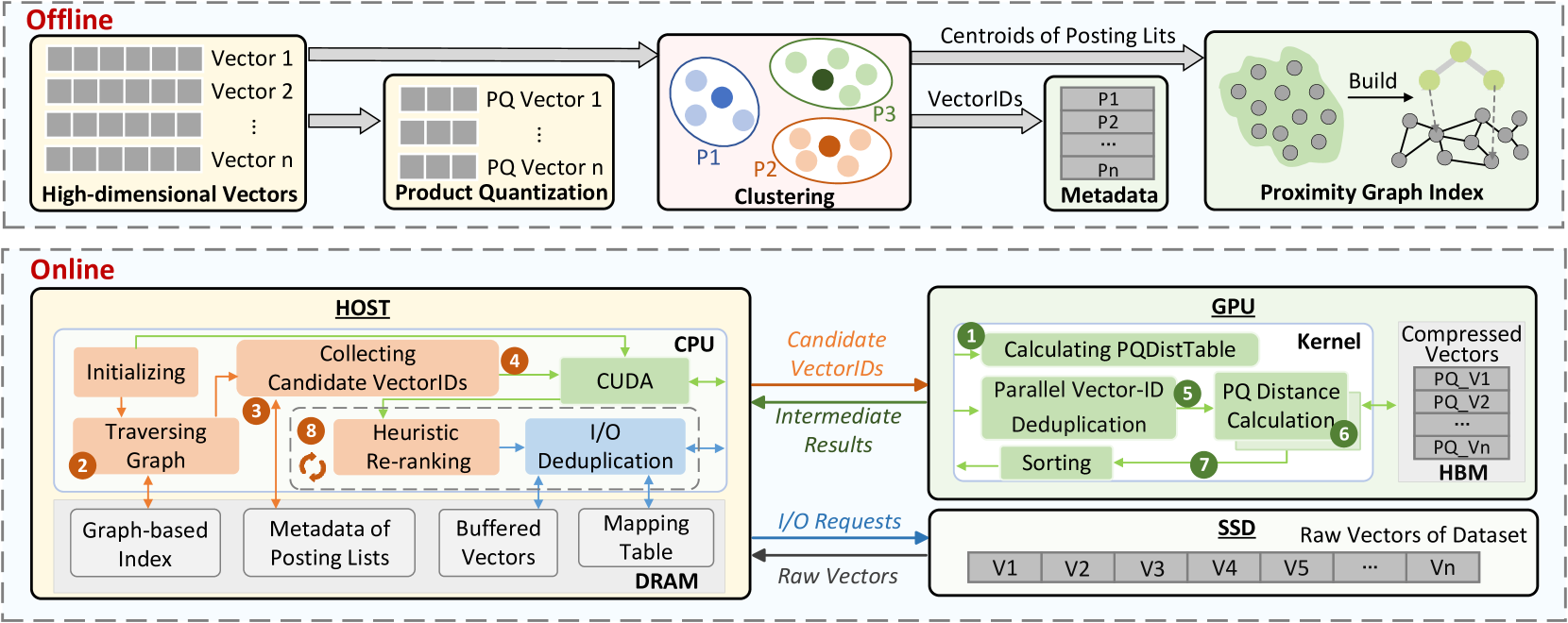
系统架构序列

在进入下面的学习之前，我们先根据上图，对架构进行一个大概的了解，我将围绕两个问题来介绍FusionANNS系统：

fusionanns中的离线层都做了些什么，在线层又做了些什么。
当一个用户查询向量进来后，都会经历哪些步骤

首先你需要知道并牢记三个概念，

PQ量化：一种压缩向量技术，就像把大文件压缩成小文件，方便存储和计算。
codebook（码本）：PQ 压缩时用到的 “字典”，里面存着每个子空间的 “标准向量”（聚类中心）。
距离表：查询时用的 “快速对照表”，提前算好查询向量和 codebook 里 “标准向量” 的距离，避免重复计算。

离线层

首先是数据分组，用分层聚类算法（比如 k-means）把所有向量分成多个 “小组”（posting lists），每个小组有一个 “中心点”（centroid）。针对边界向量（同时靠近多个聚类中心的向量），采用复制机制分配：若向量 $v$ 到聚类 $C_{i}$ 的距离满足 $Dist (v, C_{i}) \leq (1 + ϵ) \times Dist (v, C_{1})$ （其中 $C_{1}$ 是离 $v$ 最近的聚类， $ϵ$ 为距离阈值），则 $v$ 会被分配到 $C_{i}$ 中；为平衡精度与效率，每个向量最多分配到 8 个聚类。回到离线层图中，你可以看到，基于所有PostingList的centerId，采用SPTAG算法构建导航图，存储到内存中，构建时，每个新加入的质心会与最近的64个质心建立边（你可以自定义边的数量，可以为64，不够开销会变大），同时限制每个节点的最大边数，提取每个发布列表的向量ID作为元数据，注意，这里是向量的ID，不是向量的值。与导航图共同存储到内存中，此时，之前构建的发布列表就可以丢弃了，我们在cpu内存里面只保存图，而这个图里面只有id，没有值，这样就可以大幅度降低内存占用。

到这里，离线层的部分就告一段落了，下面介绍向量存储与 PQ 量化的相关内容：

原始向量：存储在 SSD 中，仅用于在线层的重排序步骤。
PQ 压缩向量：采用产品量化（PQ）技术压缩原始向量，将每个高维向量均匀划分为 M 个子空间，对每个子空间的子向量聚类生成码本（codebook）（每个子空间的聚类数为 256，对应 1 字节的聚类 ID）。每个原始向量被压缩为 M 字节的 PQ 码（每个字节对应子空间的聚类 ID），所有压缩向量存储在 GPU 的 HBM 中；由于压缩率极高（最高 95%），入门级 GPU（如 32GB HBM）可容纳十亿级数据集。具体codebook的计算以及压缩率为什么这么高，以及，这么高的压缩如何保证查询精度，这些细节因素希望可以详细的看下文说明。

在线层

在线层通过CPU与GPU的协同处理，结合离线层的哪个导航图完成高效的查询，步骤如下：首先，由GPU生成查询向量的距离表（distance table），包含查询向量各子空间与对应codebook中所有聚类中心的距离，用于后续的PQ距离计算。然后由CPU遍历内存中的导航图，找到与查询向量最接近的top-k个节点。获取到里面的id列表，仅将这些id传输给GPU，这样减少了传输量，GPU接收到这些数据后，通过并行哈希计算对ID进行去重，避免重复计算，（与下文提到的IO优化不一样），然后，GPU对于每一个向量id，从HBM里面读取对应的PQ压缩向量，根据其PQ码（子空间的聚类ID）查询距离表（Distance Table），累加各子空间距离，得到总的PQ距离，计算的时候，GPU为每一个子空间分配一个线程访问距离表，由协调线程累加结果，这一步，你就可以多线程了，很大幅度的减少距离计算所消耗的时间，换句话说，你搜索的速度会更加快！并且，你需要知道，这一步中，是根据PQ码直接拿数据的，因为导航图的维护，可以知道数据的相似度一定是和查询向量很高的，到这里，我们实际的计算量是远比暴力检索所需要的计算量少的，只计算了距离表和累加，结合GPU的速度，可以大大提高搜索速度。最后，GPU对所有的向量的PQ距离排序，返回top-n个向量ID给CPU。 CPU收到这些向量后，将top-n向量的重排序分为多个小批次（启发式重排序），每批处理后通过轻量级反馈控制模型计算变化率 (\Delta=\frac{|S_n - S_n \cap S_{n-1}|}{k})（(S_n)为当前 top-k 结果集）；若(\Delta)连续 β 次小于阈值 ε，则终止重排序，减少无效计算。

在重排序过程中，基于冗余感知 I/O 去重机制，借助优化的 SSD 存储布局（高相似向量紧凑存储在同一页），合并同一 SSD 页的 I/O 请求（intra-mini-batch）；同时利用 DRAM 缓冲区缓存已读取的 SSD 页，避免后续批次重复读取（inter-mini-batch）。最终返回 top-k 个最近邻向量给用户(这部分下面有图可以参考)。

用户查询的处理

1. GPU 生成距离表

查询向量进入系统后，GPU 按子空间计算该查询向量与 PQ 码本中所有聚类中心的距离，生成用于后续 PQ 距离计算的距离表。这一操作借助 GPU 的并行计算能力，能快速完成，为后续流程提供基础。

2. CPU 筛选候选发布列表

与此同时，CPU 遍历内存中的导航图，依据向量间的相似度，确定与查询向量最接近的 top-m 个发布列表。这里的 top-m 并非固定值，可根据实际场景灵活调整。

3. 向量 ID 收集与传输

CPU 通过查阅元数据，提取这些候选发布列表中的向量 ID，随后将这些 ID 传输给 GPU。仅传输向量 ID 而非向量内容，有效减少了数据传输量，提升了传输效率。

4. GPU 去重与距离计算

GPU 接收到向量 ID 后，先对其进行去重处理，避免重复计算。接着，从 HBM 中读取对应的 PQ 压缩向量，结合之前生成的距离表计算每个向量的 PQ 距离。计算完成后，对所有 PQ 距离进行排序，将距离最小的 top-n 个向量 ID 返回给 CPU。

5. CPU 重排序与结果返回

CPU 接收到 top-n 向量 ID 后，对其进行启发式重排序。在重排序过程中，按照优化后的存储策略从 SSD 读取原始向量，并通过冗余感知 I/O 去重机制减少不必要的 SSD 访问。最终，确定 top-k 个最近邻向量并返回给用户。

看完了，看的懵逼，看的不理解，觉得这些写的乱七八糟的，巧了，我也是这么觉得的，但是，对于论文中提到的某些功能的实现，我觉得是一种非常有意思并且值得我们落地实践的，下面的部分内容可能会为你之后优化系统的某个方面提供一些有趣的思路~。

一、量化 (PQ) 核心流程详解

alt text

1.1 Codebook 构建（离线阶段）

在 FusionANNS 系统中，量化的第一步是构建 Codebook，这一过程在离线阶段完成。假定所有的向量都是512维，有一万个这样的向量，我们将其非为八组:

取一万个向量的前64维划为第一组
取一万个向量的64-128维划为第二组
取一万个向量的128-192维划为第三组
...
取一万个向量的448-512维划为第八组

对每一组进行k=256的k-means聚类，得到256个聚类中心，即Codebook。观察下图，可以看到codebook1为一个64x256的矩阵，其中256表示256个聚类中心，64表示每个聚类中心对应的维度。

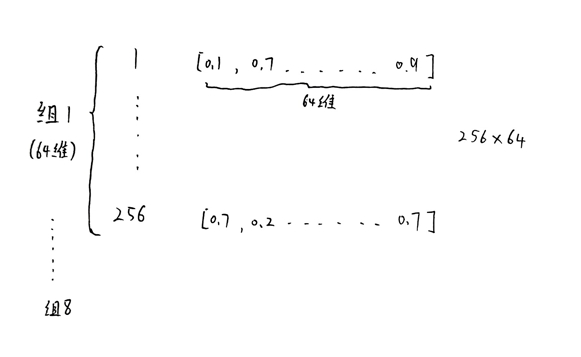
alt text

最终我们可以得到8个子码本，即8个codebook，用于下一步的PQ量化。其实现逻辑可通过以下 Python 代码示例呈现：

python

def build_codebook(vectors):
    codebooks = []
    for i in range(8):  # 8个子空间
        start_dim = i * 64
        end_dim = (i+1) * 64
        subspace = vectors[:, start_dim:end_dim]  # 提取64维子空间
        
        # 执行k-means聚类(k=256)
        centroids = kmeans(subspace, k=256)
        codebooks.append(centroids)  # 256x64矩阵
    return codebooks

从数学角度来看，子空间划分遵循公式

(\text{Group}_i = [64i+1, 64(i+1)] \quad i \in [0,7])

而每个子空间生成的聚类中心矩阵表示为(C_i \in \mathbb{R}^{256 \times 64})。通过这样的方式，为后续的向量量化奠定基础。

1.2 向量量化（在线阶段）

在线阶段，系统对输入的单个 512 维向量(X = (x_1,x_2,...,x_{512}))进行量化操作，输出 8 字节压缩编码。具体实现如下：

对于数据库中每一个512维度向量，取前1~64维为一组，切分为8组

txt

X = (x1 ... ... x8)

对于其中子向量x1（64维）与8个子码本计算欧氏距离。子码本Codebook1如下：

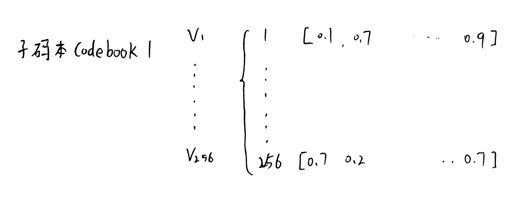
其中，欧氏距离的计算公式为：

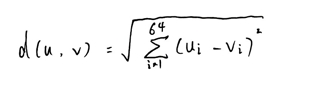
若结果为：

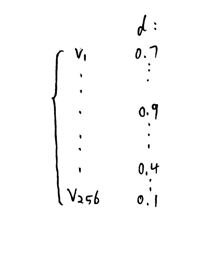
观察可得，子向量x1与CodeBook1中V256的距离最近，为0.1 记录为(256 ... ...)

同理，

子向量x2与CodeBook2的欧氏距离 d 为 xxx ,对应Vk (k∈R)
子向量x3与CodeBook3的欧氏距离 d 为 xxx ,对应Vk (k∈R)
...
子向量x8与CodeBook8的欧氏距离 d 为 xxx ,对应Vk (k∈R)

例如：

text

 1    2 3  4  5  6  7   8
(256,78,3,41,25,97,62,187)

PS:上述量化编码表示了原始向量的离散化近似表示。

综上，经过这样的量化过程，原始向量的大小从 512×4=2048 字节大幅压缩至 8 字节，实现了256:1的惊人压缩率，有效降低了内存占用，提升了数据处理效率。

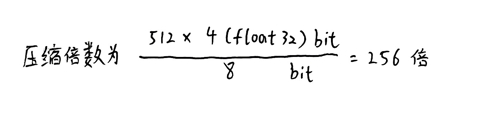
代码如下：

python

def quantize_vector(vector, codebooks):
    compressed = []
    for i in range(8):
        subvec = vector[i*64 : (i+1)*64]
        distances = [euclidean(subvec, centroid) for centroid in codebooks[i]]
        idx = np.argmin(distances)  # 找到最近聚类中心索引
        compressed.append(idx)      # 0-255整数
    return compressed  # 例：[256,78,3,41,25,97,62,187]

1.3 查询距离计算（GPU 加速）生成距离表

在查询距离计算环节，系统充分利用 GPU 加速能力。首先，对查询向量 Q 进行同样的子空间划分，得到(Q = (q_1,q_2,...,q_8))。接着，计算子空间距离表，其计算公式为：

$DistanceTable [i] [j] = | | q_{i} - C_{i} [j] | |^{2} \begin{matrix} i \in [0, 7] \\ j \in [0, 255] \end{matrix}$ 然后，根据量化编码快速计算近似距离： $Dist (Q, X) \approx \sum_{k = 1}^{8} DistanceTable [k] [{code}_{k}]$ 为进一步提升计算效率，系统采用 2048 线程并行计算（8 子空间 ×256 中心），在 V100 GPU 上，每个查询的计算耗时仅为0.0046ms，极大地加快了查询响应速度。如果不太理解，我们可以假设有一个query，对其进行PQ量化，得到PQ量化后的向量表示:

txt

Q1 = (256,78,3,41,25,97,62,187)

同样的，在PQ量化部分，我们得到了Q的八个子空间：

txt

Q = (q1 ... ... q8)

对于子空间q1，我们得到子空间q1的子码本：Codebook1，计算欧氏距离最终得到8x256的距离表：

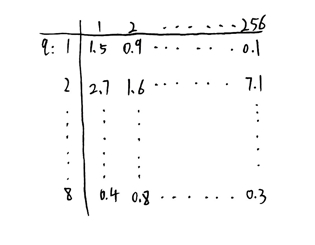
其中，

1.5表示子空间 q1 与 codebook1 中 1 号聚类中心距离为 1.5。
2.7表示子空间 q2 与 codebook2 中 1 号聚类中心距离为 2.7。
...
0.9表示子空间 q1 与 codebook1 中 2 号聚类中心距离为 0.9。

根据

txt

Q1 = (256,78,3,41,25,97,62,187)

得到：

[1][256] = 0.1
[2][78] = xx1
[3][3] = xx2
...
[8][187] = xx8

所以，总距离为0.1 + xx1 + xx2 + ... + xx8。

至此，我们对前面的内容总结一下，以便加深概念与流程的理解。

对于子码表codebook，可后台提前计算。

对于新的query，生成距离表，需计算8个子空间 x 256个中心 x 64维 = 131,072次float计算而对于现代计算机来说:

CPU:100亿次浮点运算/s --> 0.013ms
GPU:20万亿次浮点运算/s --> 0.0006ms

可用8 x 256= 2048个线程并行计算距离表......反正就是多开几个线程，算的快一些。

二、分层索引与边界优化

2.1 多层级聚类结构

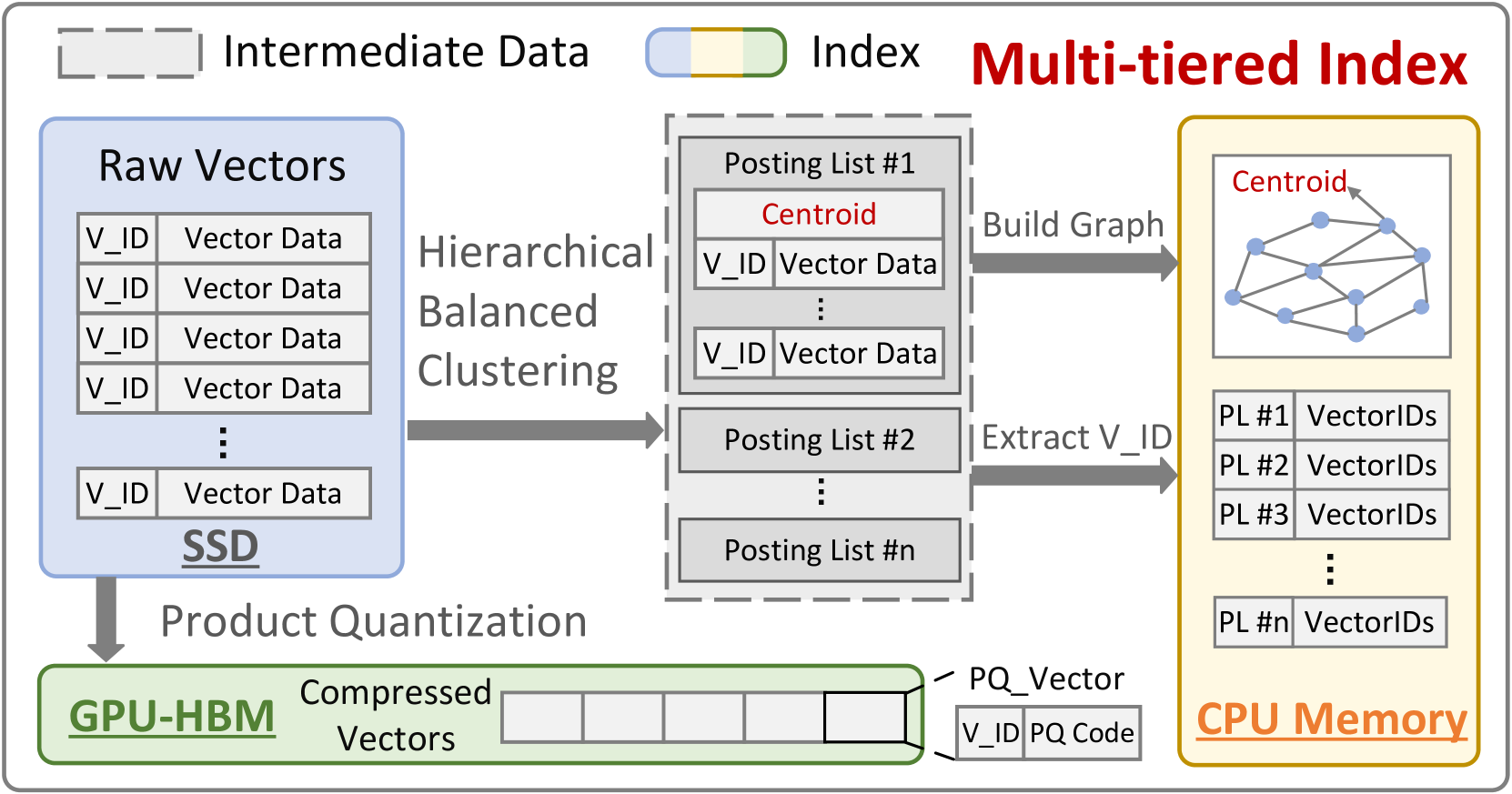对于上图，我们对每一个部分进行更加详细的解释说明：

FusionANNS 采用独特的多层级聚类结构，如下图所示。

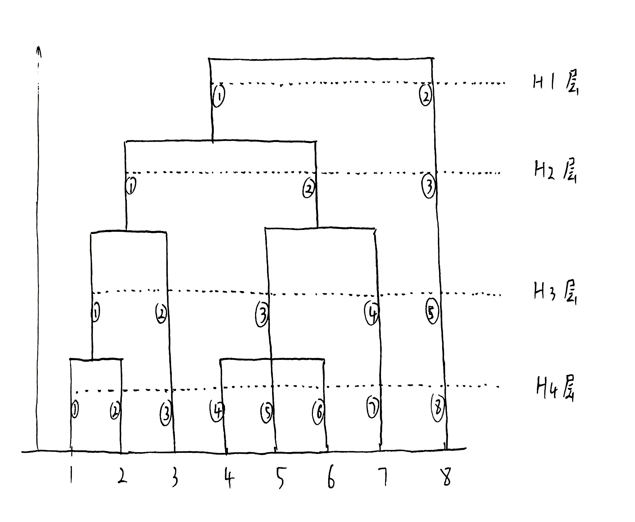FusionANNS 首先利用分层平衡聚类算法（如 k-means）对十亿级向量数据集进行迭代划分。系统将 10 亿向量依次进行 H1、H2、H3、H4 层聚类，以 H1 层为例，会聚类成 2 个质心，H2 层有 3 个质心，H3 层 5 个质心，H4 层 8 个质心，最终形成多个 Posting List，每个 Posting List 包含多个向量 ID 及其对应的向量内容。在聚类过程中，为提升聚类质量，采用复制机制处理边界向量。当向量位于多个聚类边界时，依据公式 $v \in C_{i} \Leftrightarrow D i s t (v, C_{i}) \leq (1 + ε) \times D i s t (v, C_{1})$ （其中 $v$ 代表待分配向量， $C_{i}$ 表示第 $i$ 个聚类， $C_{1}$ 是距离 $v$ 最近的聚类， $ε$ 用于平衡查询精度和效率），将边界向量分配到多个相关聚类中，每个向量最多分配到 8 个聚类。通过这种分层聚类方式，有效组织数据，缩小搜索空间。

2.2 边界向量分配算法

Specifically, when a vector lies on the boundary of multiple clusters, we assign this boundary vector to a cluster according to the following rule: 这句话的意思是：当一个向量位于多个集群的边界时，我们根据以下规则： (v \in C_i \iff \text{Dist}(v,C_i) \leq (1+\epsilon) \times \text{Dist}(v,C_1))

其中，(\text{Dist}(v, C_i)) 表示向量 (v) 到聚类 (C_i) 质心的距离，(\text{Dist}(v, C_1)) 是向量 (v) 到距离它最近的聚类 (C_1) 质心的距离，(\epsilon) 是一个用于平衡查询精度和效率的参数。

以一个具体示例来说明，假设

(\text{Dist}(v,C_1) = 0.7)
(\text{Dist}(v,C_i) = 0.3)
(\epsilon = 0.3)

则(0.3 \leq (1+0.3)\times0.7 = 0.91)，满足条件，该向量会被包含在聚类(C_i)中。

To balance the query accuracy and efficiency,each vector is assigned to eight clusters at most。通过这样的策略，单个向量可归属最多 8 个聚类，在实际测试中，相较于 SPANN，其召回率提升了 32%，显著提高了查询准确性。

三、启发式重排序算法

3.1 动态截断流程

由于 PQ 在距离计算中会导致一定的精度损失，FusionANNS 引入启发式重排序算法来优化查询结果。该算法的动态截断流程可通过以下 Python 代码实现：

python

def heuristic_reranking(candidates, query_vec, k=10, batch_size=1000, ε=0.4, β=3):

    max_heap = MaxHeap(k)  # 维护Top-k最小堆
    stability_count = 0
    
    for i, batch in enumerate(batch_split(candidates, batch_size)):
        prev_topk = set(max_heap.get_ids())  # 保存前一批Top-k
        
        # 处理当前batch
        for vec_id in batch:
            raw_vec = ssd_read(vec_id)
            dist = distance(query_vec, raw_vec)
            max_heap.push(dist, vec_id)
        
        current_topk = set(max_heap.get_ids())
        Δ = len(current_topk - prev_topk) / k  # 计算变化率
        
        if Δ < ε:
            stability_count += 1
            if stability_count >= β:  # 连续β批变化小
                break
        else:
            stability_count = 0  # 重置计数器
    
    return max_heap.get_sorted()

在这个过程中，系统将重排序过程划分为多个小批量（mini-batch）依次处理，通过不断计算变化率(\Delta)来判断结果是否趋于稳定，从而决定是否终止重排序，避免不必要的计算和 I/O 操作。

总结的有些太简单了，这里再详细的来解释：对于召回的十万Vectors我们将其分为100组，一组为1000个vector。

依次进行处理，组1处理后，进入轻量反馈控制模型，判断是否需要进行组2的处理。（看3.2）

3.2 轻量反馈控制模型变化率 Δ 的数学本质

首先我们来回顾一下为什么要做这个轻量反馈控制模型？

在 FusionANNS 中，启发式重排序（Heuristic Re-ranking）和轻量反馈控制模型（Lightweight Feedback Control Model）是为了解决 PQ 压缩导致的精度损失问题，同时避免不必要的 I/O 操作和计算开销而设计的关键机制。启发式重排序通过 “分批次处理” 避免一次性处理过多向量，而轻量控制模型通过 Δ 监控结果稳定性 —— 当新增优质向量的比例连续多次低于阈值时，说明继续处理对精度提升有限，从而终止重排序。这种机制在保证高召回率（如 Recall@10≥90%）的同时，可减少 30% 以上的 I/O 和计算开销，显著提升系统效率。

在什么时候用到呢？参考上文：

用户问题进入系统后，......，最后到了CPU 重排序与结果返回这一步,CPU 接收到 top-n 向量 ID 后，对其进行启发式重排序。在重排序过程中，按照优化后的存储策略从 SSD 读取原始向量，并通过冗余感知 I/O 去重机制减少不必要的 SSD 访问。最终，确定 top-k 个最近邻向量并返回给用户。

思想：判断下一次的处理是否会对精度造成影响。若连续的 β 次检测后，变化率 (\Delta < \varepsilon)，则安全终止重排序。其中，变化率 (\Delta) 用于衡量当前批次重排序对 Top-k 结果的优化程度，其计算公式及符号含义如下：

符号含义：

(\boldsymbol{S_n})：当前批次（第 n 批）重排序后，Top-k 向量的 ID 集合；
(\boldsymbol{S_{n-1}})：上一批次（第 n-1 批）重排序后，Top-k 向量的 ID 集合；
(\boldsymbol{S_n - S_n \cap S_{n-1}})：当前批次新增的、不在上一批次 Top-k 中的向量 ID（即 “新鲜向量”）；
(\boldsymbol{|\cdot|})：集合中元素的数量（新增向量的个数）；
(\boldsymbol{k})：最终需要返回的 Top-k 结果数量（如 k = 10）。

公式含义：(\Delta) 表示 “当前批次新增的 Top-k 向量数量” 占 “总需要的 k 个结果” 的比例。(\Delta) 越大，说明当前批次对结果的优化越明显；(\Delta) 越小，说明结果已趋于稳定。

计算公式： (\Delta = \frac{|S_n \setminus S_{n-1}|}{k} = \frac{\text{新增Top-k向量数}}{k}) 或者：

最后，小于阈值β表示，当前连续β次满足(\Delta<ε)时的子批量对Top-k的优化贡献微弱。更加详细的来说：其反映了每一批次处理后 Top-k 结果中新增向量的比例。当(\Delta>ε)时，说明结果仍在剧烈变化，需要继续处理；当(\Delta<ε)时，结果趋于稳定，系统开始准备终止；若连续(\beta)次(\Delta<ε)，则安全终止重排序。在实际应用中，该算法在不同数据集上均取得了显著效果，如在 SIFT1B 数据集上，全量重排序需要处理 40,000 个向量，而启发式重排序仅需处理 28,000 个，I/O 减少了 30%；在 DEEP1B 数据集上，同样实现了 30% 的 I/O 减少，有效提升了系统性能。

举个栗子：

比如我现在查询需要返回Top-10结果（k=10），设定( \varepsilon=0.3 )（新增占比≤30%即稳定），( \beta=2 )（连续2批稳定则终止）。

步骤1：初始化

重排序分多批次处理，每批次处理100个候选向量；
维护一个“最大堆”（记录当前Top-10向量，按距离排序）；
稳定计数器（StabilityCounter）初始为0。

步骤2：处理第1批（n=1）

上一批次（n=0）：初始堆为空，( S_0 = \emptyset )；
本批次处理100个向量，计算距离后，堆中填入10个向量，ID集合( S_1 = {v1, v2, ..., v10} )；
计算Δ：( |S_1 - S_1 \cap S_0| = 10 )（因为( S_0 )为空，所有10个都是新增），Δ=10/10=1.0；
因Δ=1.0 > ( \varepsilon=0.3 )，稳定计数器保持0，继续处理下一批。

步骤3：处理第2批（n=2）

上一批次( S_1 = {v1, v2, ..., v10} )；
本批次处理100个向量，新进入堆的向量为v11、v12（替换了v9、v10），当前( S_2 = {v1, v2, ..., v8, v11, v12} )；
计算Δ：新增向量是v11、v12（2个），Δ=2/10=0.2；
因Δ=0.2 < 0.3，稳定计数器=1，继续处理下一批。

步骤4：处理第3批（n=3）

上一批次( S_2 = {v1, v2, ..., v8, v11, v12} )；
本批次处理100个向量，新进入堆的向量仅v13（替换了v8），当前( S_3 = {v1, v2, ..., v7, v11, v12, v13} )；
计算Δ：新增向量是v13（1个），Δ=1/10=0.1；
因Δ=0.1 < 0.3，稳定计数器=2（达到β=2）；
满足终止条件，停止重排序，返回当前Top-10结果。

四、存储优化与 I/O 去重

4.1 物理存储布局优化

在存储方面，原始向量大小通常在 128 - 384 字节，而现代 NVMe SSD 的页大小为 4KB，这导致了严重的读放大问题，读放大倍数可达 10 - 32 倍。为解决这一问题，FusionANNS 对物理存储布局进行优化，如所示，系统为每个质心创建专属 Bucket，

在启发式重排序阶段获取的组N，可保证与查询query vector 高度相似，构建导航图，为每一个质心分配存储桶Bucket,存放最接近该质心的若干向量ID。

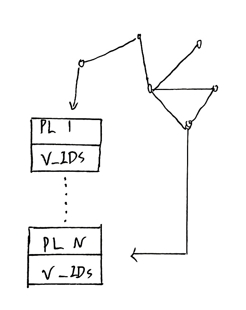
将向量按到质心距离排序填充到 Bucket 中，然后跨 Bucket 合并填充 4KB 页，以最小化碎片，从而提高存储效率和 I/O 性能。

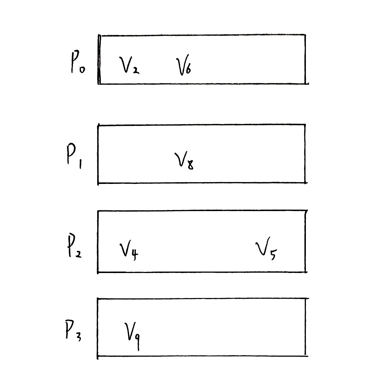
4.2 二级 I/O 去重机制

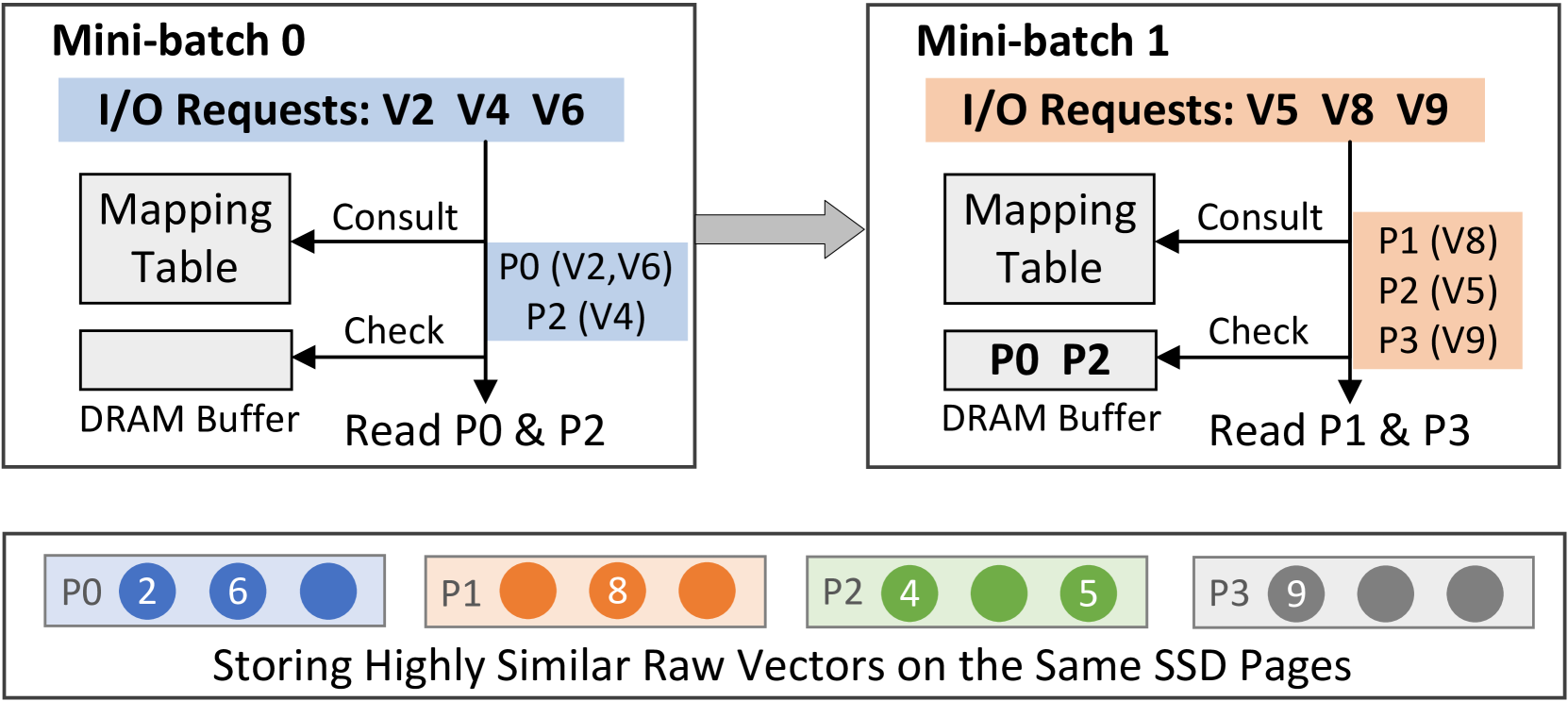
FusionANNS 还设计了二级 I/O 去重机制，包括批内合并和批间复用。在批内合并方面，以 Mini-batch 请求 V2, V4, V6 为例，系统通过映射表获取每个向量对应的页 ID，发现 V2 和 V6 位于同一页 P0，V4 位于页 P2，最终实际 I/O 操作只需读取 2 次页面（P0 和 P2），替代了原本 3 次的 I/O 请求。在批间复用方面，若 Batch0 已加载 P0（包含 V2、V6）和 P2（包含 V4）到缓存中，当 Batch1 请求 V5（位于 P2）、V8（位于 P1）、V9（位于 P3）时，由于 P2 已在缓存中，Batch1 实际只需读取 P1 和 P3 两次页面即可。通过这样的 I/O 去重机制，在实际测试中，随机存储情况下 I/O 次数为 40,000 次，数据读取量为 160MB，而经过优化后，I/O 次数减少到 30,800 次，数据读取量降低至 123MB，I/O 次数和数据读取量均减少了 23%。

五、端到端查询流程

FusionANNS 的端到端查询流程涉及多个组件协同工作，其流程如系统架构序列所示。当 Client 发送查询向量 Q 后，整个端到端流程如下：

GPU 生成距离表：GPU 首先生成查询向量的距离表，用于后续 PQ 距离计算。
CPU 定位候选簇集：同时，CPU 遍历内存中的导航图，找到与查询向量最接近的 top-m 个发布列表（而非固定的 Top-64，具体数量根据场景调整）。
CPU 收集向量 ID：CPU 查阅元数据（metadata），收集这些候选发布列表中的向量 ID。
传输 ID 至 GPU：CPU 将这些向量 ID 传输给 GPU，并调用 GPU 内核进行处理。
GPU 去重处理：GPU 接收向量 ID 后，通过并行哈希模块对其进行去重。
GPU 计算 PQ 距离：对于每个向量 ID，GPU 从 HBM 中读取对应的 PQ 压缩向量，计算其与查询向量的 PQ 距离。计算时，GPU 为每个维度分配一个线程，用于访问距离表中该维度的值，再由协调线程累加这些值得到每个候选向量的 PQ 距离。
GPU 返回 top-n 结果：GPU 对所有 PQ 距离进行排序，将距离最小的 top-n 个向量 ID 返回给 CPU。
CPU 启发式重排序：CPU 对这些向量进行启发式重排序（而非简单的动态重排序），过程中按照优化后的存储策略（将高相似向量紧凑存储以提升空间局部性）从 SSD 读取原始向量，并通过冗余感知 I/O 去重机制减少不必要的 SSD 访问（如合并同页 I/O 请求、利用 DRAM 缓冲区避免重复读取）。
返回最终结果：CPU 最终确定 top-k 个最近邻向量并返回给 Client。

上面的一大串文字，可能看起来不太容易，下面将配合着图片来解释： 对于我们所有存储在SSD中的数据，

pi'c

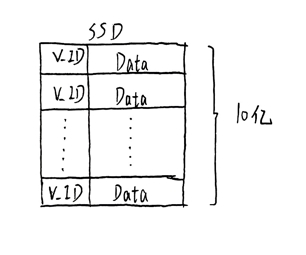
我们对其进行分层聚类得到Posting List。

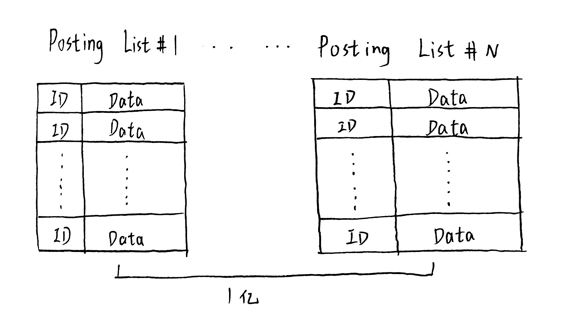
对于图中Posting List倒排索引列表，里面的ID为图的节点ID。我们根据这个倒排索引列表，构建下图：

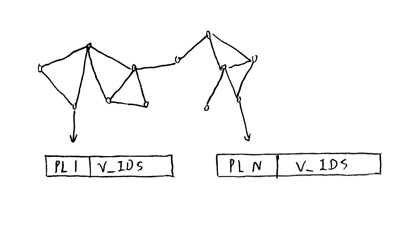
存放进入CPU，然后丢弃倒排索引列表，只保留图(注意：只存储向量的ID列表，不存实际的向量数据！)。对于新加入的点：

计算与附近Top64个最近的点的Distance并连接
类似于HNSW索引的多层小世界图
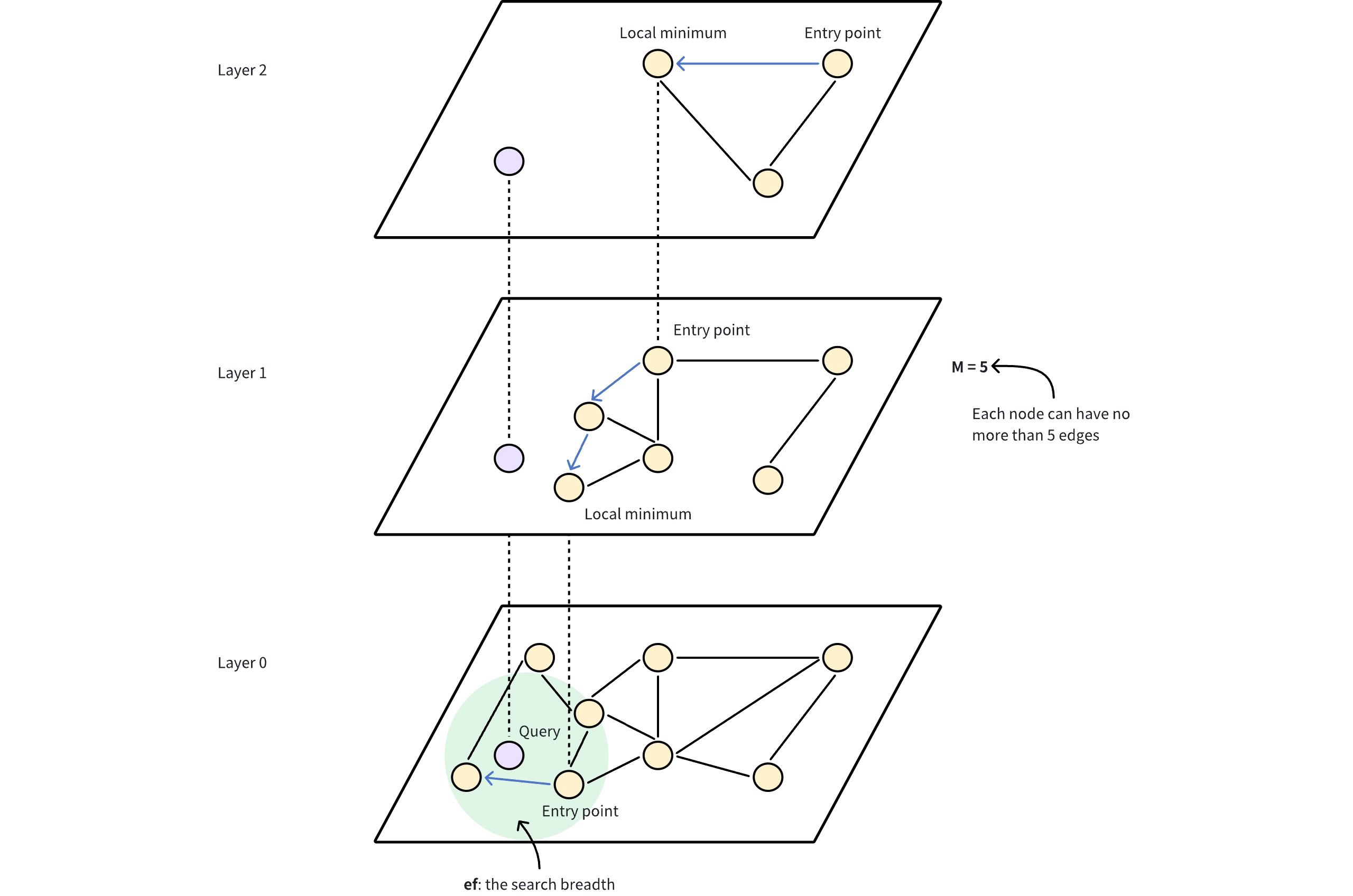
取64个PL的Meta Data PQ量化存储到GPU HBM中
GPU 根据ID List 从HBM中获取PQ量化后的组，进行Dist表的构建
其中，CPU -> SSD(根据IDs 从SSD中获取原始向量，计算精确距离，从而弥补PQ造成的精度损失，返回Top-k)

貌似有些抽象，我们回到原始的图中：

首先我们看离线层的逻辑操作：

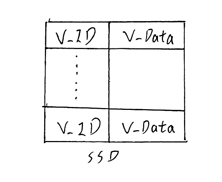
这是我们的SSD中存储的数据，包含了向量的ID和具体数据，当然，实际应用中，数据格式不可能是这么简单的，但100%包含ID 和 embedding这两个。我们有两件事情要做的：

首先：将这些数据进行PQ量化后存储到GPU HBM中，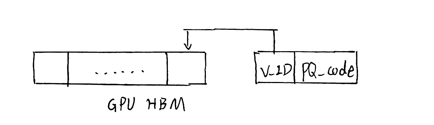

其次我们对这些数据进行分组和倒排索引（关于这一部分，请看索引部分），得到Posting List。

然后构建图并丢弃Posting List：

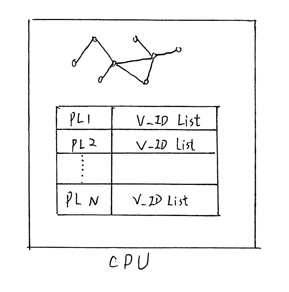
你可以看到，图中的节点ID就是Posting List中的ID。我们将这一部分数据都放到了CPU存储中，图中的每一个节点都包含：

节点ID
节点存储的向量的ID List

现在，我们离线层的数据构建就做好了，接下来，我们看在线层的逻辑操作：

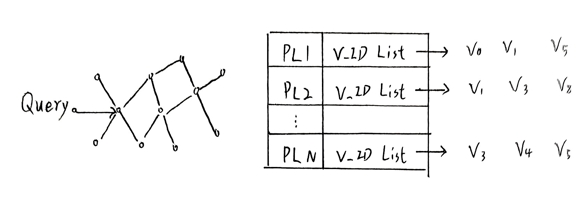
详细看过上面内容的小伙伴应该知道，这里query的计算过程，我们进入内存导航图，确定最近的PL，假设是上图中的那几个节点，我们可以组合这些ID List，可以得到：

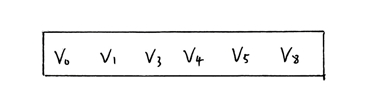
然后，GPU根据这些从CPU 传来的ID List，从自己的 HBM中获取PQ量化后的向量，得到每个V_ID (v0,v1,v3,v4 ... ... )的PQ向量。

构建距离表，

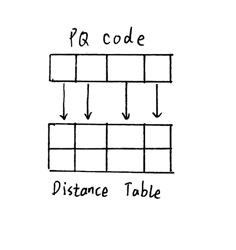
然后根据距离表，计算精确距离，返回Top-k。

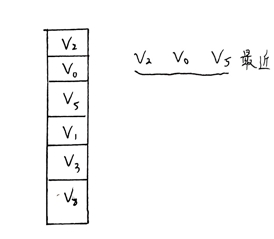
我们可以看到 v2 v0 v5 是最近的，然后就到最后了，我们将这三个ID进入I/O Engine 取SSD查询。

六、性能实验与工业价值

6.1 性能对比实验

为验证 FusionANNS 的性能优势，我们在特定实验环境下进行测试。实验环境配置为：CPU 采用 2×Xeon 64-core，GPU 为 NVIDIA V100（32GB HBM），SSD 使用 Samsung 990Pro 2TB。在吞吐量对比（QPS）方面，不同数据集下的实验结果如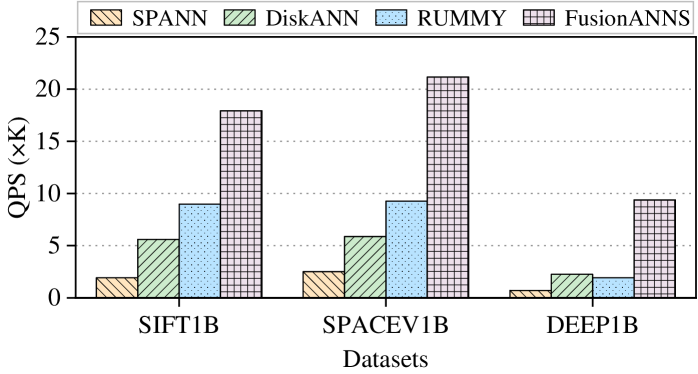吞吐量对比图所示，FusionANNS 在 SIFT1B、SPACEV1B、DEEP1B 等数据集上，相较于 SPANN 和 RUMMY，QPS 均有显著提升，展现出强大的处理能力。

6.2 工业应用场景

在工业应用中，FusionANNS 可有效优化 RAG 架构，如 [此处插入 RAG 架构优化示意图] 所示。当用户提问后，Query 经过嵌入处理进入 FusionANNS 引擎，引擎从知识库中快速检索相关向量，获取 Top-K 相关文档，为 LLM 生成回答提供准确信息。在实际应用中，原本占比 50% 的延迟降低至 10%，对于 10 亿级向量的检索，P99 延迟小于 100ms。其适用场景广泛，涵盖法律 AI（如 ChatLaw 千亿级法律条文检索）、家装设计（如 ChatHome 百万级 3D 模型检索）、金融风控（如 Xuanyuan 2.0 实时交易监测）、电商推荐（十亿级商品向量实时匹配）等多个领域，为各行业的智能化发展提供了有力支持。

七、结论与创新价值

7.1 核心突破

FusionANNS 在多个方面实现了核心突破。在存储方面，通过 PQ 压缩率达到 256:1，多层级索引将内存占用降低为 SPANN 的 1/8；计算范式上，采用 CPU-GPU 协同模式，CPU 负责导航，GPU 进行并行计算，使数据传输量减少 99%；在优化策略上，启发式重排序减少了 30% 的 I/O 操作，冗余感知存储降低了 23% 的读放大，全面提升了系统性能。

7.2 行业影响

从行业角度来看，FusionANNS 具有重要影响。在成本方面，实现千亿向量检索的硬件成本低于 $8,000；性能上，QPS 提升 13.1 倍，延迟小于 10ms P99；在生态建设中，有望成为 LLM+RAG 基础设施的标准组件，推动人工智能领域的进一步发展。最终实现：在十亿级 ANNS 中首次同时满足：高吞吐 (10k+ QPS)｜低延迟 (<10ms)｜高精度 (Recall@10>95%)｜低成本 (<$10k)，为大数据和人工智能领域的向量搜索问题提供了极具价值的解决方案。

总结

三大核心技术

多层级索引结构（Multi-tiered Indexing）

存储策略：

设备	存储内容	关键优势
SSD	原始向量（Raw Vectors）	低成本存储海量数据
GPU HBM	PQ压缩向量（高压缩比）	显存容纳十亿级向量，避免数据交换
CPU内存	向量ID列表 + 导航图（无内容）	传输量减少99%（仅传ID而非向量内容）

突破：消除CPU-GPU间冗余数据传输，解决PCIe带宽瓶颈。

启发式重排序（Heuristic Re-ranking）
- 动态截断机制：
  - 将重排序拆分为小批次（Mini-batch） 顺序执行。
  - 每批完成后计算结果改进率： [ \Delta = \frac{|S_n - S_n \cap S_{n-1}|}{k} \quad \text{(当前批与上批结果的差异率)} ]
  - 若连续β批的Δ < 阈值ε，则提前终止重排序。
- 效果：减少30% I/O和计算，精度损失<1%。
冗余感知I/O去重（Redundancy-aware I/O Deduplication）
- 优化策略：
  - 存储布局：相似向量紧凑存储（按聚类中心分桶）。
  - 去重机制：
    - 批内合并：同SSD页的I/O请求合并为单次读取。
    - 批间复用：DRAM缓存复用已加载SSD页。
- 解决痛点：原始向量（128-384B）远小于SSD页（4KB），消除读放大。

性能突破（对比SOTA系统）

对比项	vs. SSD方案 (SPANN)	vs. GPU内存方案 (RUMMY)
吞吐量(QPS)	↑ 9.4–13.1倍	↑ 2.4–4.9倍
成本效率	↑ 5.7–8.8倍 (QPS/$)	↑ 2.3–6.8倍 (QPS/$)
内存效率	↑ 13.1倍 (QPS/GB)	↑ 32.4倍 (QPS/GB)
硬件需求	单GPU (如V100) + SSD	需TB级内存 + 高端GPU

解决的核心挑战

挑战	解决方案	关键效果
GPU显存不足 → 频繁数据交换	多层级索引 + 仅传向量ID	消除CPU-GPU数据传输瓶颈
PQ压缩导致精度损失 → 需重排序	动态启发式重排序	最小化I/O+计算，保精度
SSD小粒度I/O效率低 → 读放大严重	存储布局优化 + I/O去重	减少23% I/O操作

Reference

[1] FusionANNS: An Efficient CPU/GPU Cooperative Processing Architecture for Billion-scale Approximate Nearest Neighbor Search [2] FAST 25' FusionANNS (CPU+GPU+SSD)

向量数据的存储优化与GPU加速检索 ​

1. 内存消耗 ​

2. 计算强度 ​

3. 优化方法 ​

FusionANNS 系统介绍 ​

1. 系统架构 ​

2. 性能优势 ​

流程详解 ​

离线层 ​

在线层 ​

用户查询的处理 ​

1. GPU 生成距离表 ​

2. CPU 筛选候选发布列表 ​

3. 向量 ID 收集与传输 ​

4. GPU 去重与距离计算 ​

5. CPU 重排序与结果返回 ​

一、量化 (PQ) 核心流程详解 ​

1.1 Codebook 构建（离线阶段） ​

1.2 向量量化（在线阶段） ​

1.3 查询距离计算（GPU 加速）生成距离表 ​

二、分层索引与边界优化 ​

2.1 多层级聚类结构 ​

2.2 边界向量分配算法 ​

三、启发式重排序算法 ​

3.1 动态截断流程 ​

3.2 轻量反馈控制模型 变化率 Δ 的数学本质 ​

步骤1：初始化 ​

步骤2：处理第1批（n=1） ​

步骤3：处理第2批（n=2） ​

步骤4：处理第3批（n=3） ​

四、存储优化与 I/O 去重 ​

4.1 物理存储布局优化 ​

4.2 二级 I/O 去重机制 ​

五、端到端查询流程 ​

六、性能实验与工业价值 ​

6.1 性能对比实验 ​

6.2 工业应用场景 ​

七、结论与创新价值 ​

7.1 核心突破 ​

7.2 行业影响 ​

总结 ​

三大核心技术 ​

性能突破（对比SOTA系统） ​

解决的核心挑战 ​

Reference ​

向量数据的存储优化与GPU加速检索

1. 内存消耗

2. 计算强度

3. 优化方法

FusionANNS 系统介绍

1. 系统架构

2. 性能优势

流程详解

离线层

在线层

用户查询的处理

1. GPU 生成距离表

2. CPU 筛选候选发布列表

3. 向量 ID 收集与传输

4. GPU 去重与距离计算

5. CPU 重排序与结果返回

一、量化 (PQ) 核心流程详解

1.1 Codebook 构建（离线阶段）

1.2 向量量化（在线阶段）

1.3 查询距离计算（GPU 加速）生成距离表

二、分层索引与边界优化

2.1 多层级聚类结构

2.2 边界向量分配算法

三、启发式重排序算法

3.1 动态截断流程

3.2 轻量反馈控制模型变化率 Δ 的数学本质

步骤1：初始化

步骤2：处理第1批（n=1）

步骤3：处理第2批（n=2）

步骤4：处理第3批（n=3）

四、存储优化与 I/O 去重

4.1 物理存储布局优化

4.2 二级 I/O 去重机制

五、端到端查询流程

六、性能实验与工业价值

6.1 性能对比实验

6.2 工业应用场景

七、结论与创新价值

7.1 核心突破

7.2 行业影响

总结

三大核心技术

性能突破（对比SOTA系统）

解决的核心挑战

Reference